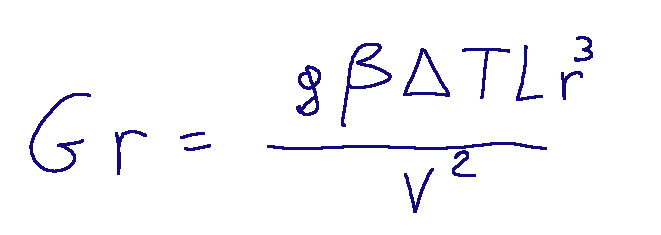~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
01-03-2024 - Physics - Dimensionless groups [EN]-[IT]
Basic concepts
In thermodynamics there are many basic concepts, they depend on what area we are in thermodynamics. Below are some of the many basic concepts.
mechanical energy equation
When we think about the mechanical energy equation we can derive it by eliminating the terms related to heat.
Assuming that we are in the stationary case and that ρ=constant we will have the following equation which coincides with the Bernoulli equation.
The formula we will obtain will be the following
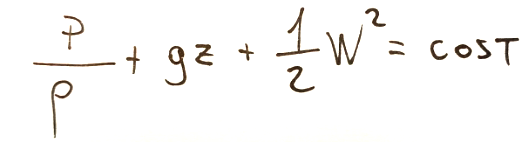
More precisely, the formula written above coincides with the Bernoulli equation, relating to the motion of a non-viscous fluid in stationary cases, with a single inlet and a single outlet, in the absence of propeller work and friction.
Pressure losses
Pressure drops are defined as the pressure difference between the extreme sections of a pipe of length L.
Gradient and divergence
The gradient of a variable, such as temperature, is an operator that transforms a scalar into a vector; the divergence of a vector, on the other hand, is an operator that transforms a vector into a scalar.
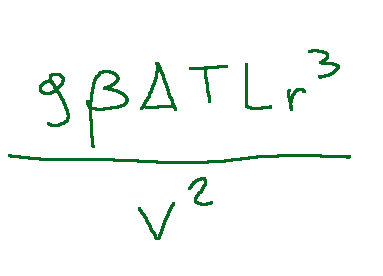
Dimensionless groups
Below is the definition of dimensionless groups for forced convection.
Convection is a heat exchange mechanism between a solid surface and a liquid or gas.
We can say that convection is a system for transporting energy through the combined action of conduction, energy storage and mixing. If we consider the matter at a molecular level, we can say that heat exchange by conduction is accompanied by internal energy transport due to the relative motion of the particles.
The forced convection equation is as follows
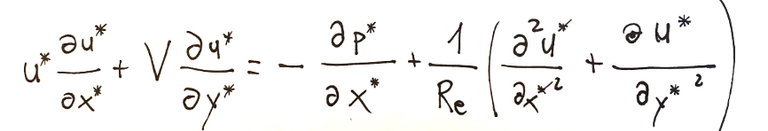
and this form of equation can be obtained by introducing dimensionless quantities into the starting equation.
See example below in which dimensionless quantities have been introduced into the starting equation.
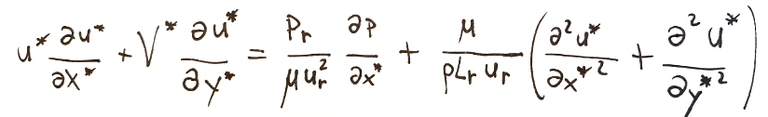
Where:
the subscript “r” indicates the reference quantities
the superscript “*” indicates dimensionless quantities.
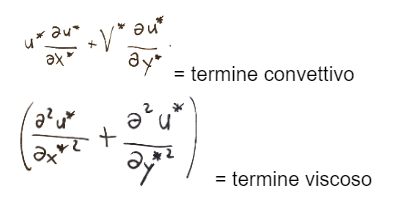
Continuing we can dimensionless the energy balance using the Prandtl number.
The Prandtl number represents the ways in which energy exchanges occur at the molecular level due to collisions and momentum.
We finally arrive at the following result.
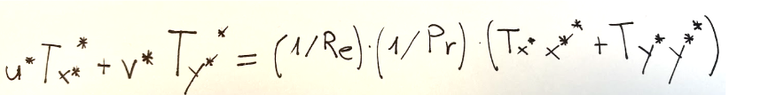
Conclusion
To dimensionless the energy balance the Prandtl number can be used. The most important thing to understand is what this number represents. The Prandtl number represents the ways in which energy exchanges occur at the molecular level due to collisions and momentum.
Request
These are concepts that in my opinion are rather elaborate and that are not developed thoroughly during the school period, in fact how many of you have heard of Prandtl's number?

01-03-2024 - Fisica - Gruppi adimensionali [EN]-[IT]
Concetti base
In termodinamica i concetti base sono molteplici, dipendono in che area siamo dalla termodinamica. Qui di seguito alcuni dei tanti concetti base.
equazione dell’energia meccanica
Quando pensiamo all’equazione dell’energia meccanica la possiamo derivare eliminando i termini legati al calore.
Ipotizzando che siamo nel caso stazionario e che ρ=costante avremo la seguente equazione che coincide con l’equazione di Bernoulli.
La formula che otterremo sarà la seguente
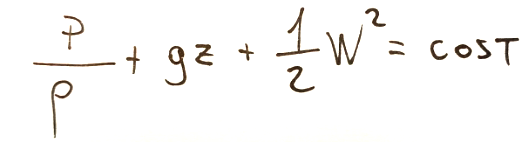
Più precisamente, la formula scritta qui sopra, coincide con l’equazione di Bernoulli, relativa al moto di un fluido non viscoso nei casi stazionari, con un solo ingresso ed una sola uscita, in assenza di lavoro d’elica e di attriti.
Perdite di carico
Le perdite di carico si definiscono come la differenza di pressione tra le sezioni estreme di una condotta di lunghezza L.
Gradiente e divergenza
Il gradiente di una variabile, ad esempio come può essere la temperatura, è un operatore che trasforma uno scalare in un vettore; la divergenza di un vettore, al contrario, è un operatore che trasforma un vettore in uno scalare.
Gruppi adimensionali
Qui di seguito la definizione dei gruppi adimensionali per convezione forzata.
La convezione è un meccanismo di scambio termico tra una superficie solida ed un liquido o un gas.
Possiamo dire che la convezione è un sistema per trasportare energia mediante l’azione combinata della conduzione, dell’accumulo di energia e del mescolamento. Se consideriamo la cosa a livello molecolare, possiamo dire che allo scambio termico per conduzione si affianca un trasporto di energia interna dovuto al moto relativo delle particelle.
L’equazione della convezione forzata è la seguente
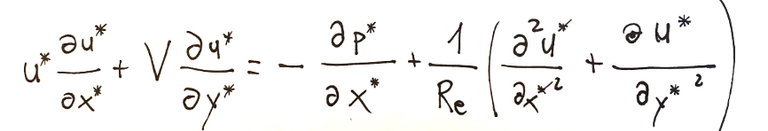
e questa forma di equazione può essere ricavata introducendo nell’equazione di partenza le grandezze adimensionalizzate.
Vedi esempio qui sotto riportato in cui nell’equazione di partenza sono state introdotte le grandezze adimensionalizzate.
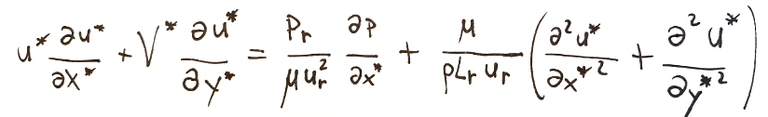
Dove:
il pedice “r” indica le grandezze di riferimento
l’apice “*” indica le grandezze adimensionalizzate.
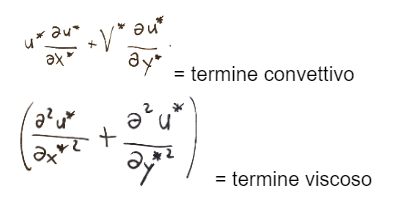
Proseguendo possiamo adimensionalizzare il bilancio dell’energia avvalendosi del numero di Prandtl.
Il numero di Prandtl rappresenta i modi in cui avvengono gli scambi di energia a livello molecolare per urti e per quantità di moto.
Arriviamo infine al seguente risultato.
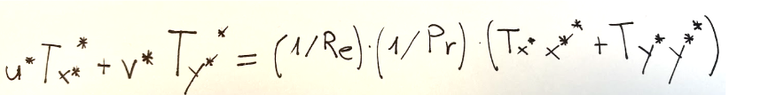
Conclusione
Per adimensionalizzare il bilancio dell’energia si può usare il numero di Prandtl. La cosa più importante da comprendere è cosa rappresenta questo numero. Il numero di Prandtl rappresenta i modi in cui avvengono gli scambi di energia a livello molecolare per urti e per quantità di moto.
Domanda
Questi sono concetti che secondo me sono piuttosto elaborati e che non si sviluppano a fondo durante il periodo scolastico, infatti in quanti di voi hanno sentito parlare del numero di Prandtl?
THE END